短時間フーリエ変換
x軸が時間、y軸が振幅を表す波形にフーリエ変換(離散フーリエ変換)を施し、その絶対値をプロットするとx軸が周波数、y軸が強度を表す。
波形の全時間に対してどれくらいの周波数がどの程度含まれているのかを知りたい場合はこれで十分。
しかし、どの時間にどれくらいの周波数が含まれているかを知りたい場合には使えない。
それを解決する手法が短時間フーリエ変換(Short -Term Fourier Transformation, STFT)である。
こちらの説明が分かりやすい。
https://www.jstage.jst.go.jp/article/jasj/72/12/72_764/_pdf
通常のフーリエ変換に対して一定の区間だけで大きさを持つ窓関数を元の波形にかけてフーリエ変換を行う。
一度フーリエ変換が終われば窓関数を一定の幅だけスライドさせて元の波形にかけてフーリエ変換を行う。
これを繰り返すことにより時間と周波数、強度の3つの関係を表す図(スペクトログラム)を作成できる。
窓関数を元の波形に対して作用させると
が窓関数でその長さを
とする。つまり、
の範囲だけ値をとり、その他は0である。
このtは窓関数の時間座標から見たときの尺度なので、元の音源に対してはとなる。
ここでは窓関数をスライドさせる幅である。一度窓関数をスライドさせるごとに
が1ずつ増加していく。
は窓関数を当てた後のスペクトログラムのフレーム数のインデックスに対応する。
これに対してフーリエ変換を施すので
となる。
この式から窓関数のサイズを大きく取るとより細かく周波数成分を調べることができる。
つまり周波数成分の分解能を高くすることができる。
周波数と時間の分解能にはトレードオフの関係があることに注意する。
wikiのExampleの比較も分かりやすい。
https://en.wikipedia.org/wiki/Short-time_Fourier_transform
スペクトログラムはx軸にを、y軸に
をとってz軸に
をプロットしたものになる。
3次元の図となるが基本的にはz軸を色の濃淡で表した2次元の図で表されることが通例である。
スペクトログラムもlibrosaで簡単に作成できる。
import librosa import librosa.display import matplotlib.pyplot as plt sr = 44100 music, sr_ = librosa.load("fanfare.wav", sr=sr) D = np.abs(librosa.stft(y)) plt.figure(figsize=(10,4)) librosa.display.specshow(librosa.amplitude_to_db(D, ref=np.max), y_axis='log', x_axis='time', sr=sr) plt.title('Power spectrogram') plt.colorbar(format='%+2.0f dB') plt.tight_layout()
- 結果

(librosa.display.specshowではsrを指定しないと意図しない値になるので注意)
Dの次元は(周波数、時間、強度)になっている。
n_fftが窓関数のサイズ。上の数式で説明した長さに対応する。デフォルト値は
n_fft=2048。
hop_lengthがスライドさせる幅。上の数式で説明した長さに対応する。デフォルト値は
hop_length=n_fft/4。
win_lengthは窓関数の中でも実際に窓関数を適用させたい長さかな?基本的にはwin_length=n_fftで、win_length<=n_fftである。
大きさをn_fft以下に設定した場合は0でパディングされる。
windowは窓関数の種類。デフォルトではhannになっている。
n_fft()をデフォルト値よりも大きくしてみる。
これは周波数成分の分解能を高くすることを意味している。
n_fft = 2048 * 2で同様の計算をすると
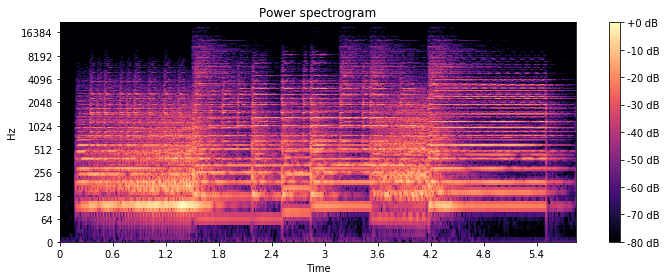
以前と比較するとより正確に周波数成分が抽出されていることが確認できます。(横縞が見えやすくなっている。)
窓関数のサイズを2倍にしたので時間は半分になっています。
もっと大きくして、n_fft = 2048 * 8でやると

より横縞がくっきり見えるようになりましたが、その分時間軸の境目の描写が曖昧になったような気がします。
この3つのスペクトルの配列を見てみると
n_fft=2048: (1025, 1007)n_fft=2048 * 2: (2049, 504)n_fft=2048 * 8: (8193, 126)
となり、時間軸の刻み幅が小さくなっていくことがわかる。 時間の分解能が低く、周波数の分解能が高くなっていることを意味している。